|
Anche qui risolviamo su un esempio pratico vediamo come risolvere la disequazione tang x > 1 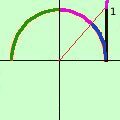
Intanto consideriamo solo una semicirconferenza (da 0° a 180°) perche' la tangente e' periodica di periodo 180° Il valore della tangente (1) e' un valore che si trova sulla verticale condotta dall'origine degli archi all'asse x la tangente sara' maggiore di 1 per valori piu' in alto del valore 1 Se dal valore 1 cosi' individuato traccio la congiungente al centro posso considerare sulla circonferenza tre archi: nell'arco a destra (quello blu) il valore della tangente e' < di 1 mentre nell'arco al centro (quello viola) il valore va da 1 a piu' infinito; invece a sinistra (quello verde) il valore della tangente va da meno infinito a zero so che il valore di 1 per la tangente corrisponde a 45° avremo quindi che la tangente e' > di 1 se l'angolo e' compreso fra 45° e 90° 45° < x < 90° e siccome siamo sul semicerchio trigonometrico dovremo considerare tutte le soluzioni che differiscono di un mezzo giro completo
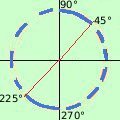
di solito quando si risolve una disequazione si preferisce indicare graficamente la soluzione con un tratto continuo dove e' verificata e con il tratteggio dove non e' verificata; inoltre conviene indicare tutte le soluzioni per il primo giro completo come vedi qui di fianco |

|

|

|

|