 Lega fra loro il seno ed il coseno permettendo di trasformare
l'uno nell'altro
Lega fra loro il seno ed il coseno permettendo di trasformare
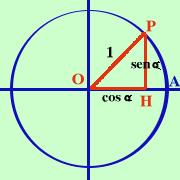
l'uno nell'altroConsideriamo una circonferenza trigonometrica (cioe' di raggio 1) e su di essa prendiamo un punto P cui corrisponda l'angolo alfa Il seno, il coseno ed il raggio formano un triangolo rettangolo, quindi, per essi, vale il Teorema di Pitagora sen2 Attenzione! Un errore abbastanza comune e' quello di confondere sen2
La relazione che abbiamo dimostrato per la circonferenza trigonometrica e' comunque valida per tutte le circonferenze Ricaviamo dalla formula trovata le formule per ricavare il seno ed il coseno sen cos scegliendo il piu' od il meno a seconda del quadrante in cui si trova l'angolo il seno e' positivo nel primo e nel secondo quadrante, negativo nel terzo e nel quarto il coseno e' positivo nel primo e nel quarto quadrante,negativo nel secondo e nel terzo Se non ti piacciono i radicali non ti preoccupare troppo: di solito vengono usati per trasformare termini che sono al quadrato e quindi va via la radice |

|

|

|

|