|
Questo teorema ci garantisce che, in una piramide regolare, il raggio del cerchio inscritto nella base e l'apotema cadono nello stesso punto di un lato Se una retta e' perpendicolare ad un piano e se dal punto di incontro prendo sul piano una retta che sia perpendicolare ad un'altra retta del piano allora l'ultima retta e' perpendicolare al piano individuato dalle prime due rette
Per mostrare che la retta r e' perpendicolare al piano individuato dai punti ABC, essendo r per ipotesi gia' perpendicolare a BC, bastera' mostrare che e' anche perpendicolare ad un'altra retta del piano cioe' alla retta AC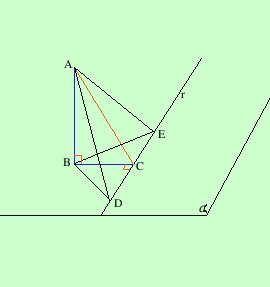 
sulla retta r da parti opposte rispetto a C considero due punti
D ed E tali che DC = CE.considero il triangolo BDE, esso ha l'altezza BC che e' anche mediana e quindi e' un triangolo isoscele ed avro' BD = BE Considero ora i triangoli rettangoli ABD ed ABE: sono rettangoli perche' le rette BD e BE passano per il punto d'incontro tra la perpendicolare ed il piano; essi, oltre l'angolo retto hanno: AB in comune BD = BE perche' appena dimostrato Quindi per un criterio di congruenza dei triangoli rettangoli avremo che i due triangoli sono congruenti ed in particolare avranno AD = AE Considero ora il triangolo ADE; esso, avendo due lati uguali AD = AE sara' isoscele e quindi la sua mediana AC sara' anche l'altezza; quindi AC e' perpendicolare a DE cioe' ad r. Essendo r perpendicolare a due diverse rette AC ed AD del piano individuato da ABC per il criterio di perpendicolarita' la retta r sara' perpendicolare al piano Come volevamo dimostrare |
BC
|
|
|
|