|
o circonferenza circoscritta ad un quadrato 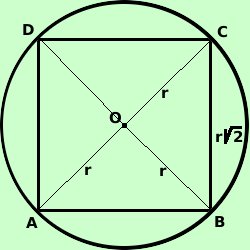 E' possibile risolvere completamente il quadrato
conoscendo il valore del raggio del cerchio circoscritto al quadrato
stesso
E' possibile risolvere completamente il quadrato
conoscendo il valore del raggio del cerchio circoscritto al quadrato
stessoInfatti la diagonale del quadrato corrisponde al diametro del cerchi quindi AC = 2r AO = r Ma anche OC = r Inoltre il triangolo BOC e' rettangolo ed isoscele E' un triangolo rettangolo perche' congiungendo il centor del cerchio con i vertici del quadrato ottengo 4 triangolo congruenti (3° Criterio di congruenza) e quindi l'angolo giro di 360° viene suddiviso nei 4 triangoli e quindi ogni triangolo ha un angolo di 90° E' un triangolo isoscele perche' le congiungenti il centro con i vertici del quadrato sono raggi Posso applicare il teorema di Pitagora per trovare il valore del lato BC BC2 = BO2 + OC2 BC2 = r2 + r2 BC2 = 2 r2
Noto il valore del lato del quadrato, per trovare il valore del raggio del cerchio circoscritto al quadrato basta fare la formula inversa, infatti, noto il valore l del lato AB avremo:
|

|

|

|

|