|
o circonferenza inscritta in un triangolo equilatero 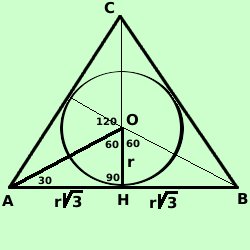 Anche in questo caso e' possibile risolvere completamente il triangolo
conoscendo solamente il valore del raggio del cerchio inscritto
Anche in questo caso e' possibile risolvere completamente il triangolo
conoscendo solamente il valore del raggio del cerchio inscrittoInfatti tracciando dal centro del cerchio le perpendicolari ai lati del triangolo equilatero e congiungendo il centro con i vertici del triangolo ottengo tre triangoli Per il teorema delle tangenti condotte da un punto esterno ad una circonferenza, le altezze di questi triangoli sono anche mediane e quindi i tre triangoli sono isosceli con un angolo al vertice di 120° (angolo giro diviso tre); Posso quindi considerare 6 triangoli tra loro congruenti: le meta' dei 3 triangoli isosceli. Ne considero uno, ad esempio AHO Esso ha: OH = r perche' raggio del cerchio circoscritto L'angolo AOH = 60° perche' meta' dell'angolo di 120° essendo l'altezza OH anche bisettrice dell'angolo AOB l'angolo AHO = 90° perche' OH e' l'altezza del triangolo AOB Quindi il triangolo AOH e' un triangolo con angoli di 30°, 60° e 90° e siccome conosco il valore del lato OH = r avremo AO = 2r
semplifico
Da norate che l'altezza CH del triangolo equilatero vale 3r infatti CH = CO + OH = 2r + r = 3r Noto il valore del lato l del triangolo, per trovare il valore del raggio del cerchio inscritto basta fare la formula inversa, infatti, noto il valore l del lato AB avremo:
|

|

|

|

|