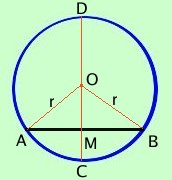
L'asse di una corda e' il diametro ipotesi    AMO^= OMB^   AM = MB    tesi   CD   diametro    Dimostrazione So per ipotesi che CD e' l'asse della corda AB quindi e' la sua perpendicolare passante per il centro ed e' anche l'insieme dei punti del piano equidistante dagli estremi. Per dimostrare che CD e' un diametro basta dimostrare che il centro O vi appartiene Il centro O della circonferenza, per definizione di circonferenza, e' equidistate da tutti i punti della circonferenza e quindi anche dagli estremi A e B della corda, cioe' O appartiene al luogo geometrico asse di AB come volevamo