|
Ricordiamoci che e' valido il quinto postulato Data una retta ed un punto fuori di essa da quel punto si puo' tracciare solo una retta parallela alla retta data Possiamo ora dimostrare che Se due rette sono parallele allora tagliate da una trasversale formano angoli alterni interni uguali Anche qui facciamo la dimostrazione per assurdo
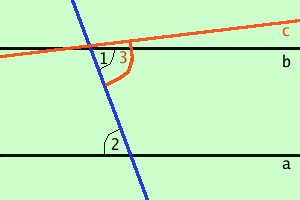Dimostrazione: Supponiamo che gli angoli non siano uguali e che, ad esempio l'angolo 1 sia piu'piccolo dell'angolo 2, allora io posso prendere, a partire dalla trasversale, un angolo 3 (in rosso) che sia uguale all'angolo 2. Ma per il criterio precedente allora la retta c sara' parallela alla retta a; per il quinto postulato, dovendoci essere una sola parallela, la retta b non puo' essere parallela alla retta a contro l'ipotesi. Quindi il criterio e' vero. Lo so benissimo che dalla figura si vede chi e' parallelo e chi no, ma tu devi immaginare le rette quasi sovrapposte e che si discostino di un centimetro dopo chilometri, io ho dovuto disegnarle cosi' per esigenze grafiche (dove lo trovo un foglio lungo 3 Km?) Avendo dimostrato sia il criterio che il criterio inverso i due fatti Rette parallele <=> Angoli alterni interni uguali saranno d'ora in poi equivalenti, cioe' se trovi in un problema che due rette sono parallele nelle ipotesi scriverai che gli angoli sono uguali e dimostrerai che gli angoli alterni interni sono uguali per dimostrare che le rette sono parallele |
|
|
|
|