Geometria di Riemann E' una delle piu' strane, ma piu' vicina delle altre alla geometria del mondo reale consideriamo come piano la superficie di una sfera consideriamo come punto l'insieme di due punti opposti sulla sfera (polo nord e sud assieme formano un punto) consideriamo come retta un qualunque cerchio massimo, (cioe' tipo l'equatore). Con queste convenzioni valgono tutti i postulati eccetto il quinto: infatti due rette qualunque sulla sfera avranno sempre un punto in comune: dove i cerchi si tagliano 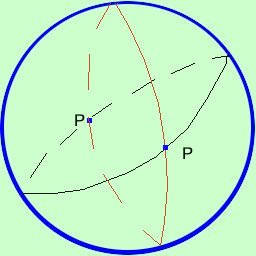e quindi non potra' mai esistere una retta parallela ad un' altra In questa geometria da un punto non si puo' mandare nessuna retta parallela