Problema Sui lati dell'angolo A si prendano due segmenti AB ed AC congruenti e, consecutivamente, altri due segmenti congruenti BD e CE. Si unisca B con E e C con D. Sia F il punto di intersezione: dimostrare che la retta AF e' la bisettrice dell'angolo A Facciamo come negli esercizi precedenti (naturalmente lo faremo solo per i primi esercizi, poi, una volta diventati esperti, abbrevieremo): Leggiamo con calma il testo cercando di capire bene tutti i termini Tracciamo una grande figura seguendo le indicazioni e segnando sulla figura stessa tutti gli elementi che sappiamo congruenti Scriviamo l'ipotesi e la tesi Partiamo dalla tesi e risaliamo fino ai dati Scriviamo lo stesso procedimento a rovescio(partiamo dall'ipotesi ed arriviamo alla tesi) Mettendo assieme quanto visto nei punti precedenti abbiamo Ipotesi AB = AC BD = CE 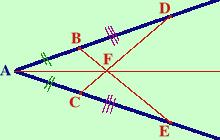tesi ^ ^ B A F = F A C 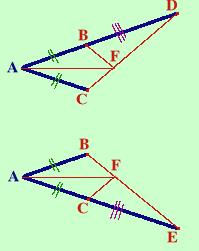Considero i triangoli ADC ed ABE (te li ho estratti dalla figura completa), essi hanno: AC=AB per ipotesi AD=AE perche' somma di segmenti congruenti L'angolo A in comune Quindi i due triangoli sono congruenti per il primo criterio di congruenza ed in particolare saranno congruenti gli angoli ADC=AEB e ABE=ACD (Ripeto la figura per farti seguire meglio il ragionamento) Considero ora i triangoli BFD e CFE, essi hanno: BD=CE per ipotesi Gli angoli BDF=CEF perche' appena dimostrato Corrispondono agli angoli ADC ed AEB Gli angoli FBD=FCE perche' supplementari degli angoli congruenti ABE=ACD come abbiamo appena dimostrato Supplementari vuol dire che con gli altri angoli formano un angolo piatto I due triangoli sono congruenti per il secondo criterio ed in particolare hanno congruenti i lati BF=CF Considero infine i triangoli ABF e ACF, essi hanno: AB=AC per ipotesi Gli angoli AF congruente perche' in comune BF=CF perche' appena dimostrato Quindi i due triangoli sono congruenti per il terzo criterio ed in particolare avranno congruenti gli angoli BAF=CAF cioe' AF e' la bisettrice come volevamo dimostrare