Dimostriamo che la figura individuata dalle 4 tangenti e' un rombo

Possiamo seguire la definizione di rombo e quindi mostrare che i lati (che abbiamo gia' visto paralleli) sono uguali oppure potremmo anche mostrare che le diagonali sono tra loro perpendicolari: siccome il problema ci richiede di utilizzare la definizione seguiamo il primo metodo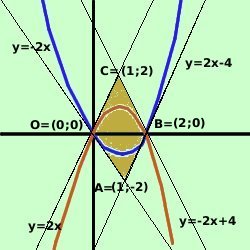

Per semplicita' rinominiamo i punti di intersezione
O A B C come da figura

Troviamo i vertici del parallelogramma come punti di intersezione fra le tangenti;
intanto conosciamo gia' 2 punti l'origine O=(0;0) ed il punto B=(2;0) in cui le parabole tagliano l'asse delle x

Troviamo ora le coordinate del punto A all'incrocio delle tangenti
y = -2x ed y = 2x -4
faccio il sistema

y = -2x
y= 2x - 4

2x - 4 = -2x
y = 2x - 4

2x + 2x = 4
y = 2x - 4

4x = 4
y = 2x - 4

x = 4/4 = 1
y = 2(1) - 4

x = 1
y = -2

quindi A=(1, -2)

Troviamo quindi le coordinate del punto D all'incrocio delle tangenti
y = 2x ed y = -2x + 4
faccio il sistema

y = 2x
y= -2x - 4

y = 2x
2x = -2x - 4

y = 2x
2x + 2x = 4

y = 2x
4x = 4

y = 2(1) = 2
x = 4/4 = 1

x = 1
y = 2

quindi D=(1, 2)

Calcoliamo ora le misure dei lati utilizzando la formula della distanza fra due punti
Punti O=(0;0) A=(1;-2) B=(2;0) C=(1;2)


distanza =		(x₂ - x₁)² + (y₂ - y₁)²


OA =		(1 - 0)² + (-2 - 0)²	=		1+4	=		5


AB =		(2 - 1)² + [0 -(- 2)]²	=		1+4	=		5

Sapendo che in un parallelogramma i lati opposti sono fra loro congruenti e' sufficiente quanto abbiamo fatto per dimostrare che si tratta di un rombo