esercizio Data la parabola y = x2 trovare le equazioni della sua tangente parallela alla retta y = 2x. Soluzione: 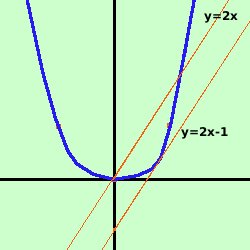prima disegniamo la parabola y = x2 e la retta y=2x. Consideriamo il fascio di rette parallelo alla retta e fra queste individuiamo la tangente facendo il sistema fascio-parabola e ponendo il delta uguale a zero considero il fascio di rette parallele alla retta y = 2x y = 2x + k Faccio il sistema fra il fascio di rette e la parabola y = 2x + k y= x2 Sostituisco il valore della y dalla prima equazione nella seconda ed ottengo l'equazione risolvente 2x+ k = x2 x2 -2x - k = 0 questa e' l'equazione risolvente il sistema: per avere due soluzioni coincidenti devo porre il delta dell'equazione uguale a zero = b2-4ac = 0 Ho a = 1       b = -2       c = -k = b2-4ac = (-2)2 - 4 (1)(-k) =0 4 + 4k = 0 4k = -4 k = -1 Quindi la tangente e' y = 2x - 1