esercizio Rappresentare graficamente la parabola di equazione y = 1/9 x2 - 4/9 x - 32/9 1) Troviamo le coordinate del vertice abbiamo a = 1/9 b = 4/9 c = -32/9 Calcoliamo la coordinata x del vertice: Vx -b - 4/9 Vx = -------- = ------- = - 2 2a 2/9 Calcoliamo la coordinata y del vertice: Vy b2 - 4 ac (4/9)2 - 4 (1/9)(-32/9) Vy = - --------------- = - ------------------------------------ = - 4   4a 4/9 Otteniamo quindi: V = ( - 2; - 4)      2) troviamo l'intersezione D con l'asse y Basta prendere come y il termine noto D = (0; -32/9) circa ( 0 ; -3,5) 3) troviamo le intersezioni con l'asse x, se esistono Devo fare il sistema fra la parabola e l'equazione dell'asse x (y=0) y = 1/9 x2 + 4/9 x - 32/9 y = 0 sostituisco 1/9x2 + 4/9 x - 32/9 = 0 y = 0 divido per 9 x2 + 4x - 32 = 0 y = 0 ottengo ottengo le soluzioni         calcoli 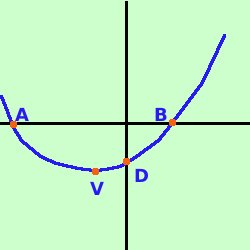x = -8            x = 4 y = 0 y = 0 quindi avremo A =(-8,0)   B=(4,0) Ora devo mettere i punti in un sistema di assi cartesiani e tracciarne la congiungente ricordando che il vertice e' sempre il punto di massimo o di minimo della curva (vuol dire che sul vertice devo fare la conca)