Equazione della parabola con asse parallelo all'asse y 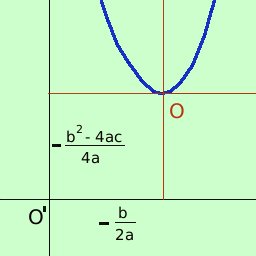Consideriamo l'equazione della parabola con vertice nell'origine O, Y = aX2 Spostiamo la nuova origine degli assi nel punto b b2 - 4 ac O' = -  -----  ;  -  --------------- 2a 4a O', faremo quindi la traslazione di coordinate b X = x + ---- 2a b2 - 4ac Y = y + ---------- 4a sostituiamo nell'equazione di partenza b2 - 4ac b 2 y + -------------- = a x + ---- 4a 2a sviluppo il quadrato e semplifico il 2 nel doppio prodotto b2 - 4ac 2bX / b2 y + -------------- = a x2 + -------  + ------- 4a 2a/ 4a2 moltiplico al secondo termine per a e semplifico ove possibile b2 - 4ac abX / ab2/ y + -------------- = a x2 + -------  + ------- 4a a/ 4a2/ ottemgo b2 - 4ac b2 y + -------------- = ax2 + bx + ------- 4a 4a Faccio il m.c.m. = 4a 4ay + b2 - 4ac 4a2x2 + 4abx + b2 ---------------------- = --------------------- 4a 4a Tolgo il denominatore ed elimino quello che posso 4ay + b2/ - 4ac = 4a2x2 + 4abx + b2/ 4ay = 4a2x2 + 4abx + 4ac Ora divido tutti i termini per 4a ed ottengo la formula finale y = ax2 + bx + c