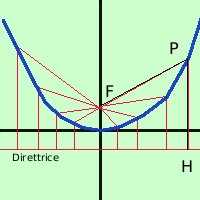
Poniamo F = (0 , p) quindi la direttrice avra' equazione y = - p Siccome devo porre PF=PH ricaviamo PF e PH Per ricavare PF uso la formula della distanza fra due punti P = (x,y)       F = ( 0,p) PF_ = (x - 0)2 + (y - p)2 = x2 + (y - p)2 Per trovare PH mi servono le coordinate di H osservando la figura vedo che la x di H e' uguale a quella di P mentre la y si trova sulla direttrice quindi vale -p P = (x,y)       H = (x, -p) Osservo che il segmento PH e' verticale quindi si puo' ottenere come differenza fra le coordinate y potevo fare anche la distanza punto retta, oppure la distanza fra due punti PH_ PH_ = | y + p |     Il modulo indica che il valore della distanza e' sempre positivo imposto l'uguaglianza PF_ = PH_ x2 + (y - p)2 = | y + p | Per togliere la radice elevo al quadrato prima e dopo l'uguale, cosi' la radice si elimina con il quadrato x2 + (y - p)2 = (y + p)2 eseguo i quadrati     Essendo un quadrato sempre non negativo posso trascurare il modulo x2 + y2 - 2py + p2 = y2 + 2py + p2 elimino i termini uguali da parti opposte dell'uguale x2 - 2py = 2py x2 = 2py + 2py x2 = 4py ricavo y 4py = x2 e, dividendo per 4p, ottengo la formula finale 1 y = ----- x2 4p Per avere la formula canonica ora basta porre 1 ----- = a 4p