Equazione canonica dell'iperbole canonica significa regolare 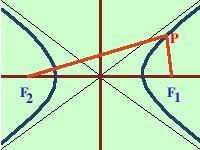Per trovare l'equazione dell'iperbole consideriamone la definizione: prendiamo un punto generico P(x,y) ed imponiamo che la differenza delle distanze di P dai due punti fissi F1(c,0) ed F2(-c,0) sia uguale a 2a Chiamiamo le coordinate orizzontali di F con +c e -c, questo perche' sviluppando l'equazione avremo bisogno di un'altra lettera (che chiameremo b) e questa comparira' nell'equazione finale; in questo modo nell'equazione finale avremo le prime due lettere dell'alfabeto: a, b PF2 - PF1 = 2a __   __ Applico la formula della distanza fra due punti nel piano ed ottengo [(x+c)2 + y2] - [(x-c)2 + y2] = 2a     E' un' equazione irrazionale quindi isolo una radice [(x+c)2 + y2] = 2a + [(x-c)2 + y2] elevo al quadrato da entrambe le parti dell'uguale    x2 + 2cx + c2 + y2 = 4a2 + 4a[(x-c)2 + y2] + x2 - 2cx + c2 + y2 Sommo i termini simili e isolo la radice dopo l'uguale     4cx - 4a2 = 4a[(x-c)2 + y2] Divido tutti i termini per 4 cx - a2 = a[(x-c)2 + y2] Elevo a quadrato da entrambe le parti     c2x2 - 2a2cx + a4 = a2[x2 - 2cx + c2 + y2] = c2x2 - 2a2cx + a4 = a2x2 - 2a2cx + a2c2 + a2y2 Termini con la x e la y prima dell'uguale, gli altri dopo l'uguale c2x2 - 2a2cx - a2x2 + 2a2cx - a2y2= a2c2 - a4 tolgo i due termini uguali e di segno opposto c2x2 - a2x2 - a2y2= a2c2 - a4 metto in evidenza la x2 prima dell'uguale ed a2 dopo l'uguale x2(c2 - a2) - a2y2 = a2(c2 - a2) ora pongo c2 - a2 = b2    posso farlo perche' c > a b2x2 - a2y2 = a2b2 divido tutti i termini per a2b2 b2x2 a2y2 a2b2 -------- - -------- = -------- a2b2 a2b2 a2b2 Semplifico ed ottengo l'equazione canonica dell'iperbole x2 y2 ----- - ----- = 1 a2 b2