|
Vediamo ora di applicare il metodo direttamente su un esempio: Trovare i punti comuni alle circonferenze x2+ y2 - 2x = 0 x2+ y2 - 4x - 2y + 4= 0 metto a sistema le due equazioni x2+ y2 - 4x - 2y + 4 = 0 sottraggo le due equazioni termine a termine; per non sbagliare prima cambiamo di segno tutti i termini della seconda equazione poi facciamo la somma in verticale -x2 - y2 + 4x + 2y - 4 = 0 ------------------------------------ // // + 2x + 2y - 4 = 0 Posso ancora semplificarla dividendola per 2 x + y - 2 = 0 Sostituisco ora questa equazione alla seconda equazione del sistema (perche' e' la piu' difficile) x + y - 2 = 0 Ricavo la x dalla seconda equazione x = 2 - y Sostituisco il valore della x nella prima equazione (io faccio tutti i calcoli, tu puoi abbreviare) x = 2 - y Eseguo i calcoli x = 2 - y x = 2 - y Divido per 2 la prima equazione x = 2 - y La prima equazione e' spuria y(y-1) = 0 ed ha soluzioni y1 = 0 y2 = 1 Sostituisco il primo valore nella seconda equazione del sistema e trovo le coordinate del primo punto
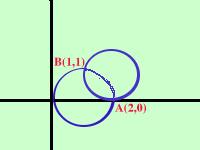
A(2,0) B(1,1) A fianco una rappresentazione grafica del problema |

|

|

|

|