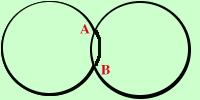
Intersezioni fra due circonferenze Osservando due circonferenze nel piano puoi vedere che, se si intersecano, hanno due punti in comune Quindi, facendo il sistema fra le due circonferenze deve essere possibile trovare le coordinate dei punti Pero' un'equazione di una circonferenza e' di secondo grado, quindi il sistema fra le due circonferenze sarebbe di quarto grado, ed io non sono capace di risolvere un'equazione di quarto grado Per risolvere il problema possiamo utilizzare una proprieta' delle equazioni: la somma o la differenza termine a termine fra due equazioni valide e' ancora un'equazione valida (per valida intendo che non deve essere ne' impossibile ne' indeterminata) Se noi sottraiamo termine a termine un'equazione dall'altra otteniamo un'equazione di primo grado che possiamo sostituire nel sistema ad una qualunque delle due equazioni di partenza e quindi il nostro sistema e' diventato di secondo grado Viene pero' da chiedersi: cosa rappresenta quest'equazione di primo grado? Ed ancora : se il sistema di partenza e' di quarto grado cosa rappresentano le soluzioni che non corrispondono ai due punti? Vediamo tutto nei particolari Determinazione dei punti di intersezione Dimostrazione teorica L'asse radicale I punti ciclici di una circonferenza