Utilizzo della geometria per risolvere algebricamente il problema Esiste una stretta equivalenza fra la soluzione algebrica e geometrica del problema e poiche' di solito la soluzione geometrica e' piu' facile ed intuitiva si puo' utilizzare questa per poter impostare l'equivalente soluzione algebrica. I punti A=(0,4) B=(-4,1), C=(-1,-3) siano tre vertici consecutivi di un parallelogramma. Trovare le coordinate del quarto vertice Dovro' costruire geometricamente un parallelogramma conoscendone tre vertici consecutivi Metodo geometrico Procedimento algebrico Traccio i tre punti 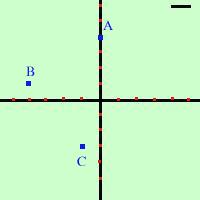Considero i tre punti: A=(0,4) B=(-4,1) C=(-1,-3) Collego il punto A col punto B 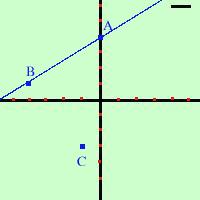Equazione della retta passante per i due punti A e B y - y1       x - x1 ------- = --------- y2 - y1       x2 - x1 Collego il punto B col punto C 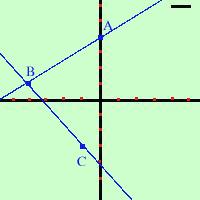Equazione della retta passante per i due punti B e C y - y1       x - x1 ------- = --------- y2 - y1       x2 - x1 Dal punto A traccio la parallela alla retta BC 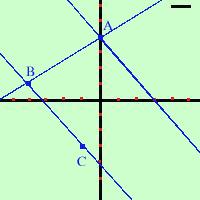Equazione della retta parallela alla retta BC passante per il punto A y - y1 = m1(x - x1) Dal punto C traccio la parallela alla retta AB 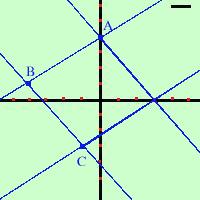Equazione della retta parallela alla retta AB passante per il punto C y - y1 = m1(x - x1) Individuo il punto d'incontro D all'incrocio delle parallele 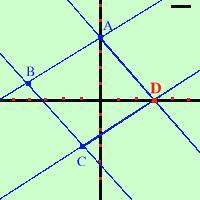Sistema fra le rette parallele trovate: ho come soluzione le coordinate del punto D Come hai visto ad ogni passaggio geometrico corrisponde un'operazione algebrica e viceversa, anzi, a tal proposito e' possibile costruire una tabella di conversione