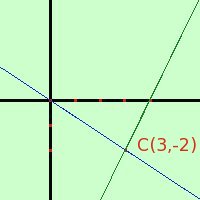
Approfondimento sui fasci di rette Si puo' definire un fascio di rette come la combinazione lineare di due rette qualunque del fascio (inserire link) Cioe' se ad esempio considero le due rette in forma implicita: 2x + 3y = 0 2x - y - 8 = 0 esse individuano il fascio di rette 2x + 3y + k(2x - y -8) = 0 A destra in blu la prima retta ed in verde la seconda C'e' un piccolo problema: dando dei valori a k possiamo trovare tutte le rette del fascio eccetto la retta 2x - y - 8 = 0, infatti tale retta si otterrebbe per un valore k = (l'infinito sara' trattato piu' avanti in analisi) allora si puo' procedere in due modi diversi: si considera come fascio l'insieme delle rette precedenti aggiungendovi la seconda retta cioe' 2x + 3y + k(2x - y -8) = 0 2x - y -8 = 0 Introduciamo due parametri e , allora il fascio di rette sara'dato da (2x + 3y) + (2x - y -8) = 0 la seconda forma puo' essere trasformata nella prima ponendo: k = ------- Consideriamo ancora il fascio 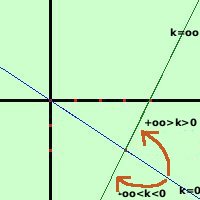2x + 3y + k(2x - y -8) = 0 2x - y -8 = 0 Osserviamo che la retta 2x + 3y si ottiene per k=0 Se diamo dei valori a k in modo ordinato (+1,+2,+3,... oppure -1,-2.-3 ,....) otteniamo altre rette che, partendo dalla prima retta, ruotando attorno al punto di intersezione, si avvicinano alla seconda retta; Ora posso avvicinarmi ad oo sia considerando valori superiori a 0 che valori inferiori: quindi abbiamo 2 possibilita' per le rette di sovrapporsi: una che nell'angolo per andare dalla prima alla seconda retta si svolge in senso antiorario e, nel nostro caso, corrisponde a valori di k>0 l'altra, invece, si svolge in senso antiorario e corrisponde, nel nostro caso, a valori di k<0. Queste considerazioni ci serviranno nella discussione del problema geometrico Vediamo ora quali sono i problemi possibili per i fasci di rette