Calcolare il valore dell'integrale
 |
x |
1 |
|
| (--------- + |
----------- |
) dx =
|
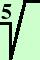 x4 x4 |
x2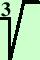 x2 x2 |
|
trasformiamo in una somma di integrali
|
 |
x |
|
 |
1 |
|
| = |
---------- |
dx + |
----------- |
dx = |
|
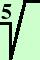 x4 x4 |
|
x2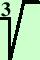 x2 x2 |
|
ora per trasformarli in integrali del tipo

|
|
xn+1 |
|
| xndx = |
----------- |
+ c |
| |
n+1 |
|
devo mettere i radicali in forma esponenziale
calcoli
=  x1/5dx + x1/5dx +
 x-8/3dx = x-8/3dx =
Quindi, applicando la regola di integrazione, ottengo
|
x1/5 + 1 |
|
x-8/3 + 1 |
|
| = |
---------- |
+ |
---------- |
= |
|
1/5 + 1 |
|
-8/3 + 1 |
|
|
x6/5 |
|
x-5/3 |
|
| = |
------ |
+ |
------ |
= |
|
6/5 |
|
-5/3 |
|
riporto in forma di radice e ribalto il denominatore (moltiplico per l'inverso del denominatore)
|
5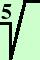 x6 x6 |
|
3 |
|
| = |
---------- |
- |
---------- |
= |
|
6 |
|
5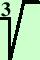 x5 x5 |
|
Estraggo di radice ed ottengo il risultato finale
|
5x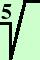 x x |
|
3 |
|
| = |
------------- |
- |
------------- |
+ c |
|
6 |
|
5x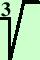 x2 x2 |
|
|