funzioni con diversa forma matematica al variare del dominio

Funzioni con diversa forma matematica al variare del dominio
Talvolta le funzioni si presentano in forma algebrica diversa a seconda del dominio su cui sono definite: tali tipi di funzione servono per meglio imprimersi i concetti di continuita' e derivabilita' e quindi vengono molto usate soprattutto in ambito teorico
Per studiarle dobbiamo restringere ogni funzione solo alla parte di piano in cui e' definita la sua forma algebrica e quindi, con un operazione di "ricucitura" ricostruire il dominio di tutta la funzione
Vediamo su un esempio come affrontare lo studio di una funzione di tale tipo.

Disegnare intuitivamente il grafico della funzione

y =	x + 1 se x < 0	Grafico
	e^x se 0 x 1
	ex se x > 1

e dire se essa e' continua e derivabile
Considero il grafico della funzione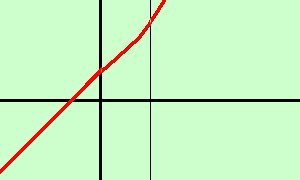

Per studiarne la continuita' e la derivabilita' devo vedere cosa succede nei punti di congiunzione, cioe' per x=0 ed x=1
Per definizione di continuita' dovra' essere

nel punto 0
lim _{x -> 0^-} x+1 = lim _{x -> 0⁺} e^x
e sostituendo 0 alla x ottengo 1=1, quindi la funzione e' continua in 0

nel punto 1
lim _{x -> 1^-} e^x = lim _{x -> 1⁺} ex
e sostituendo 1 alla x ottengo e = e, quindi la funzione e' continua in 1

quindi la funzione e' continua su tutto R

consideriamo la derivata della funzione (bastera' derivare ogni componente)

y' =		1 se x < 0
		e^x se 0 x 1
		e se x > 1

e controlliamo cosa succede in 0 ed 1
Per definizione di derivabilita' dovra' essere la derivata destra uguale alla derivata sinistra nel punto cioe'

nel punto 0
lim _{x -> 0^-} 1 = 1
lim _{x -> 0⁺} e^x = e⁰ = 1
quindi la funzione e' derivabile in 0

nel punto 1
lim _{x -> 1^-} e^x = e¹ = e
lim _{x -> 1⁺} e = e
quindi la funzione e' derivabile in 1

quindi la funzione e' derivabile su tutto R

Risultato: la funzione e' continua e derivabile su tutto R