grafici di funzioni inverse Una funzione si dice inversa di un'altra se si puo' ottenere la seconda funzione scambiando fra loro la x e la y e ricavando poi la y nella prima funzione Esempio considerata la funzione y = e x per trovarne l'inversa scambio y con x x = e y poi devo ricavare la y, siccome e' ad un esponente con e applico il logaritmo naturale a destra ed a sinistra dell'uguale log x = log (e y) logarimo ed esponenziale si elidono log x = y y = log x quindi la funzione inversa di y = e x e' y = log x intendendo con log x il logaritmo naturale di x 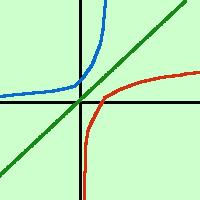Quando abbiamo due funzioni una inversa dell'altra il grafico della seconda si puo' ottenere dal grafico della prima ribaltandolo attorno alla bisettrice del primo e terzo quadrante. Nell'esempio: in blu la funzione y = e x in rosso la sua inversa y = log x ed in verde la bisettrice y = x del primo e terzo quadrante