 Si ha un asintoto orizzontale quando,
al crescere della x la y si avvicina ad un valore ben determinato.
Si ha un asintoto orizzontale quando,
al crescere della x la y si avvicina ad un valore ben determinato.in pratica c'e' l'asintoto se limx-> e l'asintoto sara' la retta orizzontale y = numero e' inoltre possibile calcolare se rispetto all'asintoto la funzione si trovi sopra o sotto sostituendo al numero dell'asintoto un numero piu' piccolo o piu' grande e vedendo se l'orizzontale relativa taglia o no la funzione, ma io penso che cio' sia inutile, in quanto in uno studio completo di funzione si hanno parecchi altri dati da cui ricavare se la funzione si avvicina all'asintoto da sopra o da sotto Facciamo anche qui un esercizio molto semplice: calcoliamo, se esiste, l'asintoto orizzontale per la funzione: 3x y = ------- x - 1 in pratica devo calcolarne il limite per x tendente ad infinito 3x limx-> x - 1 Infatti numeratore e denominatore hanno lo stesso grado ed il rapporto fra le x di grado maggiore e' 3. se non hai capito bene come ho fatto ridai un'occhiata alle forme indeterminate oppure puoi calcolare la derivata sopra e sotto e rifare il limite come abbiamo visto nelle applicazioni sulle derivate quindi la retta y = 3 sara' l'asintoto orizzontale 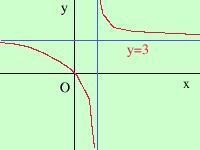 la funzione e' la stessa che abbiamo usato per l'asintoto verticale e con i dati che ho posso
cominciare ad abbozzarne un eventuale grafico
(per tracciarlo effettivamente mi mancano ancora parecchi dati):
la funzione e' la stessa che abbiamo usato per l'asintoto verticale e con i dati che ho posso
cominciare ad abbozzarne un eventuale grafico
(per tracciarlo effettivamente mi mancano ancora parecchi dati):
|

|

|

|

|