| Poiche' nei punti di flesso la tangente attraversa la curva, la curva stessa dovra' a destra ed a sinistra del punto avere una concavita' di tipo diverso, quindi la determinazione del flesso e' legata alla In pratica basta calcolare la derivata seconda e porla uguale a zero. Se nei punti in cui si annulla la derivata seconda la derivata terza e' diversa da zero avrai un punto di flesso. Successivamente puoi determinare con lo studio della derivata seconda se la concavita' e' verso l'alto o verso il basso per tracciare la curva Facciamo un esempio semplice:troviamo gli eventuali flessi della funzione y = x3 - 3x2 + 4 calcolo la derivata prima y' = 3x2 - 6x calcolo la derivata seconda yII = 6x - 6 pongo la derivata seconda uguale a zero 6x - 6 = 0 6x = 6 x=1 Calcolo le coordinate del punto sostituendo 1 alla x nella funzione di partenza f(1) = 13 - 3·12 + 4 = 1 - 3 + 4 = 2 il punto F(1,2) e' un probabile punto di flesso Per vedere se e' un flesso calcolo la derivata terza yIII = 6 si tratta di un flesso posso inoltre calcolare la tangente di flesso con la formula y - y0 = m(x - x0) essendo x0 ed y0 le coordinate del punto di flesso F(1,2) ed m il valore della derivata prima nel punto y - 2 = -3(x - 1) y = -3x + 3 + 2 y = -3x + 5 ora per meglio determinare il punto di flesso ne studio la concavita'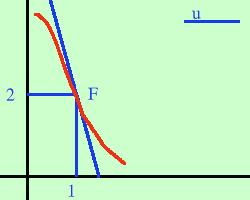 
studiando il segno della derivata seconda:yII > 0 6x - 6 > 0 6x > 6 x > 1 per x < 1 avremo la concavita' verso il basso mentre per x > 1 avremo la concavita' verso l'alto come da figura di fianco (le proporzioni non sono troppo rispettate) Se vuoi cimentarti con un esempio un po' piu' complicato |
|
|
|
|