| a) non esiste oppure b) esiste ma risulta di valore diverso dal limite E' comunque possibile eliminare tale discontinuita' attribuendo alla funzione in quel punto il valore del suo limite a) caso in cui la funzione non esiste e' gia' stato visto nelle forme indeterminate: ad esempio la funzione y= (x2-4) / (x-2) non esiste nel punto 2 ed il suo limite in tale punto vale 4; attribuendo 4 al valore della funzione in quel punto la discontinuita' e' eliminata b) caso in cui la funzione ha valore diverso dal suo limite: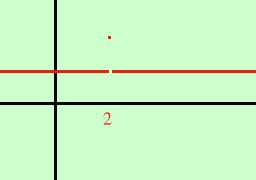 
l'esempio classico
di questa discontinuita' e' la funzione impulso:1 per x  2 y = 2 per x = 2 Batera' assegnare alla funzione il valore 1 anche nel punto 2 per eliminare la discontinuita' Simile a questa ma piu' famosa e' la funzione in due variabili delta di Kroneker cosi' definita: 0 se i j  = 1 se i=j |
|
|
|
|