Teorema della maggiorante e della minorante (Teorema dei "carabinieri") Il nome esatto sarebbe quello sopra, ma anche in alcuni testi scolastici ho visto chiamare questo teorema col secondo nome, che rende bene l' idea del teorema stesso: il teorema dice questo 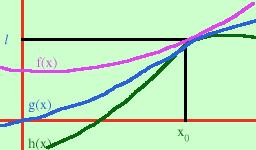Se abbiamo tre funzioni, la prima maggiore delle altre due (maggiorante) e la terza minore delle altre due (minorante) allora se sia la prima che la terza funzione tendono ad un limite finito l allora anche la seconda deve tendere allo stesso limite Inutile dire che la prima e la terza funzione fanno da carabinieri e prendono in mezzo la seconda per portarla in prigione nel limite Dirlo in forma matematica e' un po' piu' laborioso Se abbiamo tre funzioni: y=f(x)      y=g(x)      y=h(x) tali che f(x)≥g(x)≥h(x) se abbiamo inoltre che limx->x0 f(x)=l      e      limx->x0 h(x)=l allora vale anche limx->x0 g(x)=l Per un accenno di dimostrazione posso dire che prendendo un intorno completo che contenga l per f(x) e prendendo un altro intorno completo che contenga l per h(x) siccome g(x) e' compresa fra le due funzioni bastera' considerare l'intervallo intersezione dei due intorni per avere un intorno completo di l per la funzione g(x)