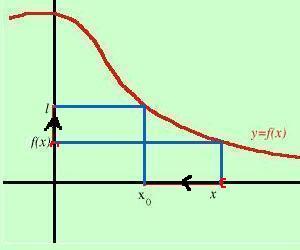
 Ora quando considero il limite limx->x0 f(x)=l invece di
considerare tutto un intervallo che contenga x0 possiamo considerarne un intorno destro (sinistro) ed in tal caso
sull'asse y corrispondera' un intorno destro o sinistro di l ma cio' non cambiera' nulla: infatti allo stringersi
dell'intervallo sull'asse delle y corrispondera' lo stringersi dell'intorno sull'asse delle x.
Ora quando considero il limite limx->x0 f(x)=l invece di
considerare tutto un intervallo che contenga x0 possiamo considerarne un intorno destro (sinistro) ed in tal caso
sull'asse y corrispondera' un intorno destro o sinistro di l ma cio' non cambiera' nulla: infatti allo stringersi
dell'intervallo sull'asse delle y corrispondera' lo stringersi dell'intorno sull'asse delle x.
Cioe' quando f(x) si avvicina ad l x si avvicina ad x0 Definizione matematica: Si dice che la funzione y=f(x) ammette limite finito destro l per x tendente ad x 0+ e si scrive: limx->x0+ f(x)=l se esiste un numero positivo |f(x)-l|< Note: x tendente ad x0+ significa che mi avvicino ad x da destra, cioe' dalla parte dei valori positivi |

|

|

|

|