Trasformare un numero complesso dalla forma normale alla forma trigonometrica
Per trasformare il numero dalla forma tipica alla forma trigonometrica devo tener presenti le formule:
-
 =
=  (a2+b2) (a2+b2)
-
a =
 cos
cos
 b =
b =
 sen
sen

faccio il rapporto
| b |
|
 sen
sen
 |
|
| --- |
= |
------------- |
= tang  |
| a |
|
 cos
cos
 |
|
quindi
|
b |
tang  = = |
--------- |
|
a |
Vediamo il procedimento su un paio di esempi:
considero il numero complesso
z = a + ib = 1 + i
per trasformarlo in forma trigonometrica
z =
 (cos (cos  + i sen
+ i sen  ) )
devo trovare il valore di 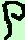 e e 
- Dalla relazione
 =
=  (a2+b2) (a2+b2)
ho:
a = 1 b = 1
Quindi
 =
=  (12+12) = (12+12) =  2 2
-
Dalle relazioni
a =
 cos
cos
 b =
b =
 sen
sen

ottengo
| b |
|
 sen
sen
 |
|
| --- |
= |
------------- |
= tang  |
| a |
|
 cos
cos
 |
|
quindi
tang  = 1/1 = 1 = 1/1 = 1
L'angolo minore la cui tangente vale 1 e' 45° o preferibilmente
 /4 /4
ottengo:
z = 1 + i =
 2 (cos 2 (cos  /4
+ i sen /4
+ i sen  /4 ) /4 )
considero il numero complesso
z = a + ib = 3 + i 3 3
devo trasformarlo in forma trigonometrica
z =
 (cos (cos  + i sen
+ i sen  ) )
-
Dalla relazione
 =
=  (a2+b2) (a2+b2)
ho:
a = 3 b =  3 3
Quindi
 =
=  [32+( [32+( 3)2] = 3)2] =  (9 + 3) = (9 + 3) =  12 = 2 12 = 2 3 3
-
Dalla relazione
|
b |
tang  = = |
--- |
|
a |
ho
|
 3 3 |
tang  = = |
--------- |
|
3 |
L'angolo minore la cui tangente vale 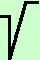 3 /3 e' 30° o preferibilmente 3 /3 e' 30° o preferibilmente
 /6 /6
ottengo:
z = 3 + i  3 =
2 3 =
2 3 (cos 3 (cos  /6
+ i sen /6
+ i sen  /6 ) /6 )
|



