Risolvere la seguente equazione esponenziale
x x = x =  x x
Per risolverla cerchiamo di togliere la potenza applicando ad entrambe i termini l'operazione di logaritmo (a base generica e quindi non la indico)
log
x x = log x = log  x x
Per la regola del logaritmo di una potenza e ricordando che
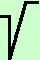 x = x1/2 ottengo x = x1/2 ottengo
|
1 |
|
 x log
x = x log
x = |
--- |
log x |
|
2 |
|
Porto i termini prima dell'uguale
|
1 |
|
 x log
x - x log
x - |
--- |
log x = 0 |
|
2 |
|
Raccolgo ora log x
|
1 |
|
(log x) ( x - x - |
--- |
) = 0 |
|
2 |
|
Questo e' un prodotto che e' zero quando uno dei due fattori e' zero, quindi la mia equazione si scompone nelle due equazioni
|
|
|
1 |
|
| log x = 0 |
|
 x - x - |
--- |
= 0 |
|
|
|
2 |
|
- Risolvo la prima
log x = 0
Il logaritmo vale zero se l'argomento vale 1 quindi
x = 1
- Risolvo la seconda
|
1 |
|
 x - x - |
--- |
= 0 |
|
2 |
|
Porto il termine noto dopo l'uguale
|
1 |
 x = x = |
--- |
|
2 |
E' un'equazione irrazionale : elevo a quadrato entrambe i membri ed ottengo
Verifico: se sostituisco 1/4 nell'equazione di partenza ottengo
1/2 - 1/2 = 0
che e' vero quindi la soluzione e' accettabile
Ottengo quindi le due soluzioni
|