devo risolvere il sistema: x(2-x) -------------- > 0 3(2+x) x(2-x) -------------- < 1         Calcoli 3(2+x) Risolvo separatamente le due disequazioni poi metto a sistema i risultati Risolvo la prima x(2-x) -------------- > 0 3(2+x) e' un prodotto e quoziente di termini: pongo ogni termine maggiore di zero e considero gli intervalli dove il calcolo dei segni mi da' un risultato posuitivo; 3 posso trascurarlo perche' certamente positivo Se hai bisogno di un ripasso 1° termine: x > 0 2° termine: 2 - x >0 3° termine: x + 2 >0 ottengo 1° termine positivo: x > 0 2° termine positivo: x < 2 3° termine positivo: x > -2 Faccio il grafico Indico i valori positivi con una linea continua ed indico i negativi con una linea tratteggiata: Per sapere il segno del totale controllo i segni con la regola del prodotto (ti ricordo che il quoziente e' un prodotto visto alla rovescia e che la regola dei segni e' la stessa per il prodotto ed il quoziente) 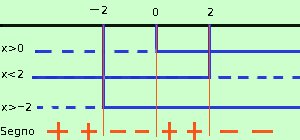Siccome cerco dove la frazione e' maggiore di zero ho come risultato: x < -2 V 0 < x < 2 Risolvo la seconda x(2-x) -------------- < 1 3(2+x) cioe' spostando 1 prima dell'uguale         Nota bene! x(2-x) -------------- - 1 < 0 3(2+x) ora posso fare il minimo comune multiplo prima dell'uguale 2x - x2 - 3(2+x) ------------------------- < 0 3(2+x) -x2 + 2x - 6 - 3x ------------------------- < 0 3(2+x) -x2 - x - 6 ---------------------- < 0 3(2+x) cambio di segno il numeratore e di verso l'equazione x2 + x + 6 ---------------------- > 0 3(2+x) e' una frazione maggiore di zero: pongo numeratore e denominatore maggiori di zero e considero gli intervalli dove i segni sono concordi Se hai bisogno di un ripasso Numeratore: x2 + x + 6 > 0         Calcoli Denominatore: 2 + x >0 posso trascurare il 3 perche' certamente positivo ottengo Numeratore positivo: sempre positivo Denominatore positivo: x > -2 Faccio il grafico indico i valori positivi con una linea continua ed indico i negativi con una linea tratteggiata: Per sapere il segno della frazione controllo i segni con la regola del prodotto (la regola dei segni e' la stessa per il prodotto ed il quoziente) 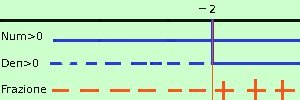Siccome cerco dove la frazione e' maggiore di zero ho come risultato: x > -2 Ora metto a sistema i due risultati x < -2 < V 0 < x < 2 x > -2 Faccio il grafico (e' un sistema quindi devo prendere le soluzioni comuni ad entrambe le disequazioni) 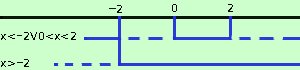Ottengo come risultato: 0 < x < 2