|
Risolvere la seguente disequazione logaritmica log3 (2-x) < log3(2+x) - log3 x + 1 Come prima cosa poniamo le condizioni che gli argomenti dei logaritmi siano positivi: devono valere le condizioni 2 - x > 0 2 + x > 0 x > 0 cioe', sviluppando: x < 2 x > -2 x > 0 Trasformiamola ora nella forma log3(espressione) < 0 Porto tutti i termini prima del minore log3 (2-x) - log3(2+x) + log3 x - 1 < 0 ricordo che 1=log33 log3 (2-x) - log3(2+x) + log3 x - log33 < 0 e, per i teoremi sui logaritmi, posso scrivere 
0 < x < 2 Mettendo assieme questa relazione con le condizioni per la realta' dei logaritmi ho il sistema x > -2 x > 0 0 < x < 2 Riporto i dati su un grafico, e prendo i valori comuni a tutte le disequazioni indico i valori accettabili con una linea continua ed indico i non accettabili con una linea tratteggiata 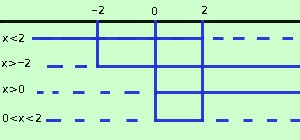
Ottengo quindi 0 < x < 2 |