Disequazione elementare del tipo
F(x) >  G(x)
Dobbiamo risolvere:
F(x) > G(x)
Il ragionamento da fare e' il seguente:
- Il termine sotto radice (radicando) deve sempre essere maggiore o uguale a zero
G(x)  0
- Essendo il radicale definito positivo (o nullo) anche il primo termine (essendo maggiore del secondo) dovra' essere positivo
F(x) > 0
- Il quadrato del primo termine dovra' essere maggiore del quadrato del secondo termine (infatti finora abbiamo supposto che sono entrambe positivi ma non che il primo e' maggiore del secondo)
[ F(x)]2 > G(x)
Quindi l'espressione si trasforma nel sistema
G(x)  0
F(x) > 0
[ F(x)]2 > G(x)
E la soluzione del sistema fornira' le soluzioni della disequazione
se abbiamo F(x)  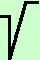G(x)
allora il nostro sistema diventera'
G(x) 0
F(x) 0
[ F(x)]2 G(x)
Infatti siccome il primo termine puo' essere uguale al secondo anche la seconda e terza disequazione del sistema avranno il maggiore od uguale
Vediamo ora un paio di esercizi:
|
