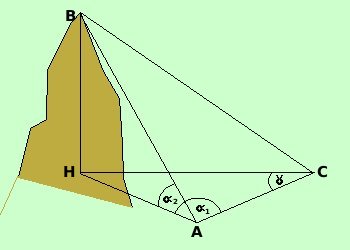
base di riferimento orizzontale Supponiamo che il segmento AC sia orizzontale: in tal caso il triangolo ACH giace sul piano orizzontale. Misuriamo La distanza AD L'angolo HAC = 1 L'angolo ACH = L'angolo BAH = 2    (angolo di aelevazione da A) Posso prima risolvere il triangolo ACH per trovare il valore di AH poi nel triangolo rettangolo AHB conosco, oltre l'angolo retto, un angolo ed un lato quindi posso risolverlo e trovare BH Considero il triangolo ACH ne conosco due angoli ed un lato e quindi posso risolverlo: Angolo AHC = 180° - (1 + ) possiamo calcolare AH con il teorema dei seni AH ---------- sen AC =  ---------------------------    sen [180° -(1 + )] e, per la relazione sugli angoli supplementari AH ---------- sen AC =  ---------------------------    sen (1 + ) Quindi otteniamo AH = AC sen  --------------    sen (1 + ) Considero poi il triangolo rettagolo BAH Per le relazioni sui triangoli rettangoli ho BH = AH tang 2 e quindi la mia formula diventa BH = AC sen tang 2  ----------------------    sen (1 + )