Altezza di una torre. Piede della torre sul piano dell'osservatore e non accessibile 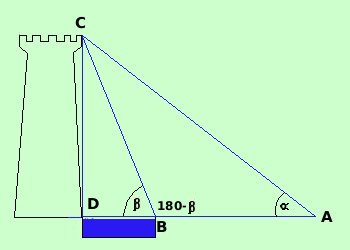Supponiamo di non poter raggiungere la torre nel punto D perche' c'e' un fossato pieno d'acqua Allora fisso un punto B, punto piu' vicino alla torre che posso raggiungere e ci spostiamo, allontanandoci dalla torre, fino ad un puntoA Calcoliamo la distanza AB e misuriamo gli angoli BAC e CBD Se l'angolo CBD = allora l'angolo CBA = 180° - e possiamo risolvere il triangolo ABC l'angolo BCA = 180° - (180° - ) - = 180° - 180° + - = - Per il teorema dei seni posso calcolare BC BC --------- sen AB =  -----------    sen (-) e quindi BC = AB sen   -----------    sen (-) Se ora considero il triangolo rettangolo BCD ne conosco l'ipotenusa ed un angolo oltre all'angolo retto, quindi posso risolverlo e trovare CD Per le relazioni sui triangoli rettangoli un cateto e' uguale all'ipotenusa per il seno dell'angolo opposto e quindi abbiamo CD = CB sen = AB sen sen   --------------------    sen (-) Esercizio supponiamo di spostarci dal punto B di 30 metri AB = 30 m e di avere i valori degli angoli =40° =70° e quindi ho CD = CB sen 70° = AB sen 40° sen 70°   --------------------------    sen (70°-40°) AB sen 40° sen 70° = -----------------------------  = sen 30° 30m·0.642788·0.9396926  ---------------------------------  = 0.5 = 36.241388 m 36,2 m E' importante fare i calcoli con molti decimali e arrotondare solamente il risultato finale, altrimenti, se arrotondassi all'inizio, l'errore potrebbe compromettere il risultato