|
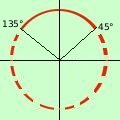
Risolvere la disequazione 2 sen x cos x - 2sen x > porto tutti i termini prima dell'uguale 2 sen x cos x - 2sen x - sono 4 termini, raccolgo a fattor comune; raccolgo 2senx fra i primi due termini e - 2 sen x (cos x - 1) - siccome ho raccolto - raccolgo ora tutta la parentesi (cos x - 1) (cos x - 1) (2 sen x - E' un prodotto: sara' maggiore di zero quando i fattori avranno segno concorde (cioe' quando entrambe i fattori sono positivi oppure sono entrambe negativi) Pongo in un sistema entrambe i fattori ponendoli maggiori di zero e trovo gli intervalli dove i segni sono concordi un piccolo ripasso 2 sen x -
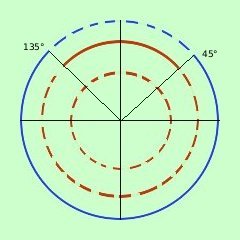
Ora cerco le soluzioni concordi della prima e della seconda disequazione (cioe' dove entrambe le disequazioni sono verificate oppure dove sono entrambe non verificate): riporto all'interno i due grafici trovati Indico in blu a linea continua dove le soluzioni sono concordi, in blu a linea tratteggiata dove sono discordi Raccogliendo ho quindi le soluzioni 0° < x < 45° U 135° < x < 360° |
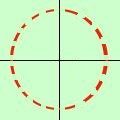 cos x - 1 > 0
cos x - 1 > 0