esercizio

Risolvere la disequazione

sen 4x > cos 2x

il primo angolo e' 4x, il secondo e' 2x riduciamo tutto a 2x (formule di duplicazione)

2 sen 2x cos 2x > cos 2x

portiamo tutto prima dell'uguale

2 sen 2x cos 2x - cos 2x > 0

Raccogliamo cos 2x a fattor comune

cos 2x (2 sen 2x - 1) > 0
E' un prodotto: sara' maggiore di zero quando i fattori avranno segno concorde (cioe' quando entrambe i fattori sono positivi oppure sono entrambe negativi)
Pongo in un sistema entrambe i fattori maggiori di zero e trovo gli intervalli dove i segni sono concordi      un piccolo ripasso
cos 2x > 0
2 sen 2x - 1 > 0
  • risolvo la prima
    cos 2x > 0
    so che il coseno e' positivo tra 0° e 90° ed anche tra 270° e 360°, quindi
    0° < 2x < 90° U 270° < 2x < 360°
    con U indico l'unione degli intervalli
    pero' io cerco l'angolo x e quindi dividiamo per 2
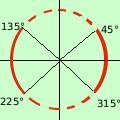
    0° < x < 45° U 135° < x < 180°
    inoltre siccome dividendo per 2 ottengo che ho la periodicita' di 180° dovro' anche considerare
    180° < x < 225° U 315° < x < 360°

    Mettendo assieme
    0° < x < 45° U 135° < x < 225° U 315° < x < 360°
    a destra la rappresentazione grafica

  • risolvo la seconda
    2 sen 2x - 1 > 0
    ricavo sen 2x
    2 sen 2x > 1
    sen 2x > 1/2
    so che il seno e' superiore ad 1/2 per gli angoli tra 30° e 150° quindi posso scrivere
    30° < 2x <+ 150 pero' io cerco l'angolo x e quindi dividiamo per 2
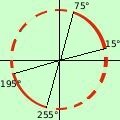
    15° < x < 75°
    inoltre siccome dividendo per 2 ottengo che ho la periodicita' di 180° dovro' anche considerare
    195° < x < 255°
    Mettendo assieme
    15° < x < 75° U 195° < x < 255°




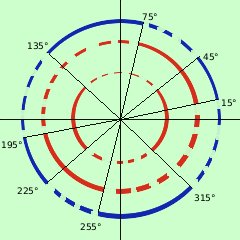
Ora cerco le soluzioni concordi della prima e della seconda disequazione: riporto all'interno i due grafici trovati


Indico in blu a linea continua dove sono concordi, in blu a linea tratteggiata dove sono discordi


Raccogliendo ho quindi le soluzioni

15°<x <45° U 75°<x <135° U 195°<x<225° U 255°<x<315°