cos x = m Anche qui cerchiamo di capire come risolverla con un esempio numerico Bisogna dire anche qui che il termine dopo l'uguale puo' avere solamente i valori da -1 a +1 perche' il cerchio trigonometrico ha raggio 1 Prendiamo l'equazione: 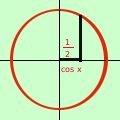1 cos x = --- 2 Il valore del coseno (1/2) e' un valore che si trova sull'asse orizzontale del cerchio trigonometrico 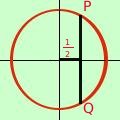Se considero il valore 1/2 sull'asse orizzontale ad esso possono corrispondere due angoli (archi): uno in alto ed uno in basso rispetto all'asse orizzontale 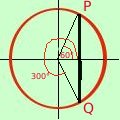so che il valore di 1/2 per il coseno corrisponde a 60° quindi il primo angolo sara' 60° ed il secondo sara' 360° - 60° = 300° Siccome le soluzioni saranno sempre 2 angoli con estremi P e Q simmetrici rispetto all'orizzontale si preferisce indicare le soluzioni come x = 60° + k 360° E se il valore che abbiamo non corrisponde ad uno dei valori in tabella cosa si deve fare? Questo fatto sara' generale: la soluzione dell'equazione cos x = n sara' sempre data dai due angoli x = ° e siccome siamo sul cerchio trigonometrico dovremo considerare tutte le soluzioni che differiscono di un giro completo x = ° + k 360° con k numero naturale ( k = 0, 1, 2, 3, 4, ...) Naturalmente la formula per l'angolo in radianti invece che in gradi e' equivalente x = + 2k con k numero naturale ( k = 0, 1, 2, 3, 4, ...)