|
sen 72°
|
|
|
tang
72°
|
---------- |
= |
|
cos
72°
|
|
|
 (10 +
2 (10 +
2 5) 5) |
| ---------------- |
|
4 |
|
|
|
= |
---------------------- |
= |
|
-1 +
 5 5 |
| -------- |
| 4 |
|
|
numeratore per l'inverso del denominatore
 (10 +
2 (10 +
2 5) 5) |
| = ----------------------- |
|
4 |
|
· |
| 4 |
| --------------- = |
-1 +
 5 5 |
|
semplifico il 4 al numeratore ed al denominatore e sotto scrivo prima il positivo e poi il negativo
 (10 +
2 (10 +
2 5) 5) |
| = ----------------------= |
 5 - 1 5 - 1 |
|
ora devo razionalizzare: moltiplico sopra e sotto per
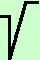 5 + 1 5 + 1
 (10 +
2 (10 +
2 5) 5) |
| = ---------------------- |
 5 - 1 5 - 1 |
|
· |
 5 + 1 5 + 1 |
| ---------------------- = |
 5 + 1 5 + 1 |
|
sotto moltiplico i denominatori ( e' un prodotto notevole)
sopra porto
(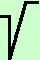 5 + 1)
dentro la radice grande (elevando al quadrato) 5 + 1)
dentro la radice grande (elevando al quadrato)
 [( [(
 5 + 1)2(10 +
2 5 + 1)2(10 +
2 5)] 5)]
|
| = ------------------------------------- = |
( 5)2 - 12 5)2 - 12
|
|
 [(5 + 1
+2 [(5 + 1
+2 5)(10 +
2 5)(10 +
2 5)] 5)]
|
| = ------------------------------------- = |
|
5 - 1
|
|
 [(6
+2 [(6
+2 5)(10 +
2 5)(10 +
2 5)] 5)]
|
| = ------------------------------------- = |
|
4 |
|
 (60
+ 12 (60
+ 12 5 +
20 5 +
20 5 + 20) 5 + 20)
|
| = ------------------------------------- = |
|
4 |
|
 (80
+ 32 (80
+ 32 5) 5)
|
| = ------------------------------------- = |
|
4 |
|
metto in evidenza 16 per poi estrarlo di radice
 16(5
+ 2 16(5
+ 2 5) 5)
|
| = ------------------------------------- = |
|
4 |
|
estraggo di radice
4 (5
+ 2 (5
+ 2 5) 5)
|
| = -------------------- = |
|
4 |
|
semplifico per 4 sopra e sotto ed ottengo il risultato finale
 (5
+ 2 (5
+ 2 5) 5)
|
|
|