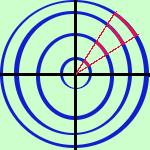
Misura di archi ed angoli Se voglio misurare un arco di circonferenza con un angolo posso farlo in modo semplice, piu' difficile e' misurarlo in centimetri perche' a circonferenze diverse corrispondono misure lineari diverse, mentre io ho bisogno di una misura valida sempre per tutte le circonferenze 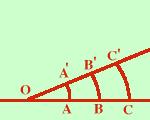Posso osservare che la misura sara' la stessa se prendo come riferimento il raggio della circonferenza: poiche' tutte le circonferenze sono simili se prendo come unita' di misura il raggio tutti gli archi avranno lo stesso valore Gli archi sono AA'     BB'     CC'     I raggi corrispondenti sono OA      OB      OC      La misura, sempre identica, sara' AA'     BB'     CC'     ----- =  ----- =  ------ OA      OB      OC     Al solito dovrei mettere la linea sopra gli archi ed i raggi per indicare che e' una misura; per me sarebbe piuttosto complicato farlo, quindi non lo faro' ma mi scuso per l'imprecisione Allora tutta la circonferenza misurera' indifferentemente 360° oppure 2 raggi essendo la misura della circonferenza 2r due pigreco corrisponde circa a 6,28 raggi cioe' se il raggio e' un centimetro la circonferenza sara' lunga circa 6,28 centimetri 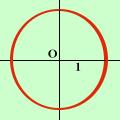Siccome tutte le misure saranno fatte rispetto al raggio, potremo, per semplicita', considerare come circonferenza tipo su cui fare le formule la circonferenza di raggio 1 che sara' chiamata Circonferenza trigonometrica L'angolo corrispondente al raggio chiamato anche angolo radiante corrispondera' circa a 57° e rotti 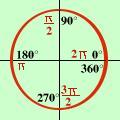La corrispondenza fra angoli ed archi sara'    -----   2  3 ----   2    2 90° 180° 270° 0°=360° Oltre i 360° i punti della circonferenza tornano su se stessi, quindi diciamo che i valori sulla circonferenza sono periodici di periodo 360° come se la circonferenza fosse una spirale i cui bracci vanno esattamente sui bracci precedenti. quindi ad esempio se hai 480° dovrai dire 480° = 480° - 360° = 120° cioe' tutti gli angoli dovranno essere riportati al primo giro della circonferenza: se l'angolo e' superiore a 360° dovrai togliere 360° una volta, due volte, tre volte,... finche' il risultato sia un angolo inferiore a 360°; ad esempio se devo considerare l'angolo di 1520° 1520° = 1520° - 360° = 1160° = 1160° - 360° = = 800° = 800° - 360° = 440° = 440° - 360° = 80° considero l'angolo di 80°