Parallelepipedo Particolare importanza fra i vari prismi avranno i prismi con base un parallelogramma Chiameremo un tale prisma Parallelepipedo I parallelepipedi saranno, grosso modo, nello spazio l'equivalente dei parallelogrammi nel piano; da notare che tutte le facce del parallelepipedo saranno parallelogrammi e la facce opposte saranno sempre congruenti Come nel parallelogramma parleremo di diagonale del parallelepipedo considerando la congiungente due vertici opposti; tutte le diagonali saranno congruenti fra loro; inoltre, come nel parallelogramma, le diagonali si incontreranno tutte nello stesso punto che le dividera' a meta'. In figura ho segnato solamente due diagonali (i segmenti in rosso) Come dalla definizione delle pagine precedenti diremo che il parallelepipedo e' retto se ha gli spigoli perpendicolari alla base Particolare importanza fra i parallelepipedi ha il parallelepipedo rettangolo che oltre essere retto ha come base un rettangolo (e quindi tutte le facce, basi comprese, saranno rettangoli)    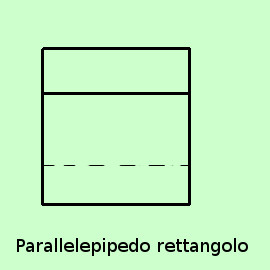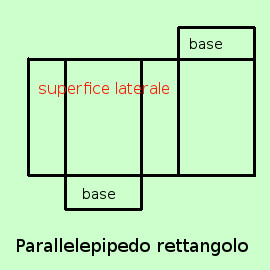              Se guardi l'ultima figura vedi che non e' molto chiara: infatti per mostrarti il rettangolo non ho potuto mettere la figura in prospettiva; per ovviare a questo inconveniente d'ora in poi, in caso di figure non chiare mostreremo le figure anche come espanse nelle facce: l'ultima figura precedente si potrebbe rappresentare come nella figura qui di fianco a destra; Per ragioni di spazio, nella figura a destra, alcune dimensioni sono state ridotte 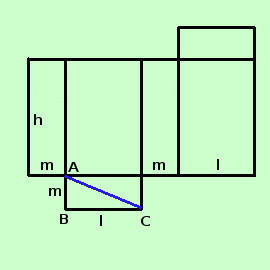Come ultimo argomento dela pagina vediamo di calcolare il valore della diagonale del parallelepipedo rettangolo; Per capirci meglio stavolta metto la figura in prospettiva; a destra la figura sviluppata nelle sue superfici traccio una diagonale in rosso; in blu traccio la proiezione della diagonale sulla base Essendo un parallelepipedo rettangolo la base e' un rettangolo e quindi per calcolare la diagonale di base AC possiamo applicare il teorema di Pitagora AC2__=   AB2__+ BC2__=   l2 + m2 Ora per calcolare il valore della diagonale AD del parallelogramma possiamo applicare il teorema di Pitagora sul triangolo ACD AD2__= AC2__+ CD2__= (AB2__+ BC2__) + CD2__= l2 + m2 + h2 quindi possiamo concludere che la diagonale d di un parallelepipedo rettamgolo e' uguale alla radice quadrata della somma dei quadrati delle tre dimensioni d =   l2 + m2 + h2