In un angoloide la somma delle facce e' minore di un angolo giro Dimostriamo che in un angoloide ogni faccia e' minore di un angolo giro Intuitivamente: se fosse un angolo giro il bordo dell'amgoloide si appiattirebbe diventando un piano e l'angoloide sarebbe un semispazio Dimostriamolo per un triedro; per un qualunque angoloide bastera' prolungare i lati di un opportuno poligono generatore fino ad ottenere un triedro e successivamente usare il teorema che una faccia e' minore della somma delle altre due se vuoi approfondire Ipotesi P(a,b,c) e' un triedro Tesi aPe^+   aPc^+  bPc^< Angolo giro 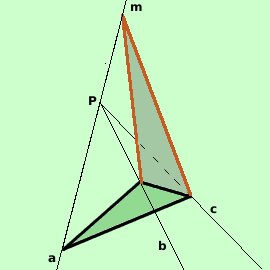Consideriamo il triedro P(a,b,c) considero la generatrice Pa e oltre P la considero come retta m e quindi considero il triedro P(b,c,m) Per esso vale bPc^< bPm^+ cPm^ sommiamo ad entrambe i membri gli angoli aPb^+ aPc^ otteniamo bPc^+ aPb^+ aPc^ < bPm^+ cPm^+ aPb^+ aPc^ ordiniamo per capire meglio aPb^+ bPc^+ cPa^ < (aPb^+ bPm^)+ (aPc^+ cPm^) Pero' sappiamo che vale (per costruzione: l'abbiamo costruito noi) (aPb^+ bPm^) = angolo piatto (aPc^+ cPm^) = angolo piatto e quindi posso scrivere aPb^+ bPc^+ cPa^ < angolo giro come volevamo