Criterio di perpendicolarita' fra piani
condizione necessaria
Mostriamo che la condizione e' necessaria: prendiamo una
retta che giaccia sul piano 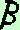 e tale retta sia perpendicolare al piano
e tale retta sia perpendicolare al piano  ; mostriamo che il piano ; mostriamo che il piano 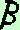 e' perpendicolare al piano e' perpendicolare al piano

 Consideriamo una retta BA, giacente su
Consideriamo una retta BA, giacente su 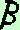 e perpendicolare al piano e perpendicolare al piano  ; ;
Il piano 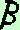 , avendo in comune con , avendo in comune con  il punto A avra' in comune
tutti i punti di una retta r passante per A. il punto A avra' in comune
tutti i punti di una retta r passante per A.
Conduciamo
per A, sul piano  , una
retta perpendicolare ad r: sia AC , una
retta perpendicolare ad r: sia AC
Il piano individuato dai punti ABC taglia i due piani  e e 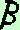 secondo due rette AB e AC tra loro perpendicolari e quindi i
due piani
secondo due rette AB e AC tra loro perpendicolari e quindi i
due piani  e e 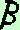 risultano tra loro perpendicolari
secondo la definizione. risultano tra loro perpendicolari
secondo la definizione.
Come volevamo
Come corollario possiamo dire che se una retta e' perpendicolare ad
un piano dato allora qualunque piano passante per tale retta e' perpendicolare
al piano dato
|
 Consideriamo una retta BA, giacente su
Consideriamo una retta BA, giacente su