Considerazioni generali Vediamo ora come definire la perpendicolarita' fra una retta e un piano. 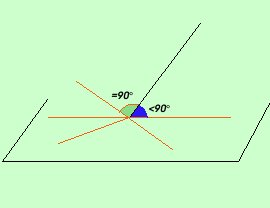Logicamente, se noi prendiamo una retta che incida un piano, se questa e' obliqua formera' tanti angoli diversi con le rette del piano passanti per il punto di incontro e tra questi potremo distinguerne due retti come si puo' facilmente vedere prendendo una penna ed il registro di classe e provando varie inclinazioni. In figura l'angolo in blu e' minore di 90° mentre l'angolo in verde e' di 90° Tra tutte le posizioni della retta pero' ve ne sara' una in cui la retta stessa sara' perpendicolare a tutte le rette del piano passanti per il punto di incontro. Viene quindi spontaneo dare la seguente definizione Si dice che una retta e' perpendicolare ad un piano se e' perpendicolare a tutte le rette del piano passanti per il loro punto di incontro 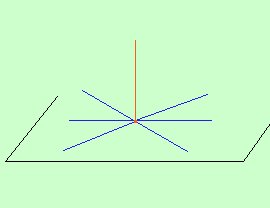Naturalmente per vedere se una retta e' perpendicolare ad un piano non possiamo considerare tutte le rette passanti per il punto di incontro fra la retta ed il piano, pertanto dovremo prendere una scorciatoia cioe' trovare un criterio che ci permetta di vedere con un numero finito di passaggi se una retta e' effettivamente perpendicolare ad un piano