|
Definiscono i legami fra gli enti geometrici Oltre quelli gia' validi per il piano (che ti consiglio di ripassare) valgono: 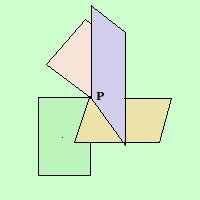 Per un punto passano infiniti piani (stella di piani) 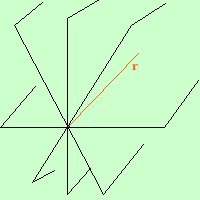 Per una retta passano infiniti piani (fascio proprio di piani) Da notare che, anche se i piani appartenenti alla stella di piani ed al fascio di piani sono entrambi infiniti, deve esistere qualche differenza tra loro, perche' nella stella di piani ci saranno tutti quelli di un fascio proprio di piani per ciascuna retta passante per quel punto E' la stessa differenza che c'e' fra i punti di una retta ed i punti di un piano: sono entrambe infiniti ma fra i due tipi di infinito deve esistere qualche differenza 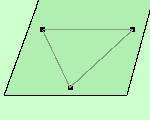
Per tre punti non allineati passa un solo piano 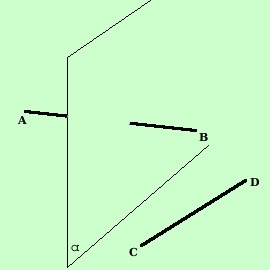
Dato uno spazio ed un piano il piano divide lo spazio in due parti (semispazi) tali che presi due punti nello stesso semispazio il segmento che li unisce non taglia il piano mentre se prendiamo due punti in semispazi opposti il segmento che li unisce taglia il piano In figura i punti C e D sono nello stesso semispazio, mentre A e B sono in semispazi opposti |

|

|

|

|