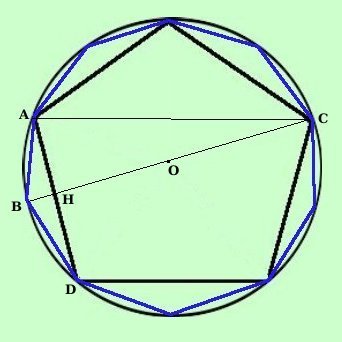
Lato del pentagono regolare Calcoliamo ora la misura del lato del pentagono regolare Considero il triangolo rettangolo ABC (rettangolo perche' inscritto in una semicirconferenza) AH e' l'altezza relativa all'ipotenusa di tale triangolo so che vale AB__=   r ( 5   - 1) 2 BC = 2r Applico il primo teorema di Euclide al triangolo ABC BH : AB = AB : BC BH = AB2 ------- BC BH__=   r2 ( 5   - 1)2 1 ·   2r 4 Moltiplico i denominatori e sviluppo il quadrato BH__=   r2 (5 + 1 - 2 5 ) 8r BH__=   r (6 - 2 5 ) 8 evidenzio il 2 al numeratore per semplificarlo con il denominatore BH__=   2r (3 - 5 ) 8 BH__=   r (3 - 5 ) 4 Ora per trovare il valore di AH applico il teorema di Pitagora al triangolo ABH AH2 + BH2 = AB" AH2 = AB2 - BH2 BH__=   r2 ( 5   - 1)2 r2 (3 - 5)2 - = 16 4 = 4r2(5 - 1)2 - r2 (3 - 5)2 = 16 Sviluppo i quadrati = 4r2(5 + 1 - 25) - r2 (9 + 5 -65) = 16 = 4r2(6 - 25) - r2 (14 -65) = 16 = 24r2 - 8r25 - 14r2 + 6r25) = 16 = 10r2 - 2r25 = 16 estraggo di radice r2 /16 AH__= r --- 4 (10 - 25) Ora moltiplico per 2 e trovo il valore del lato AD del pentagono regolare inscritto. AD__=   r --- 2 (10 - 25) E' possibile calcolare anche l'apotema del pentagono regolare