|
Vale il teorema: In poligoni simili i perimetri stanno tra loro come i rispettivi lati Cioe' se i due pentagoni 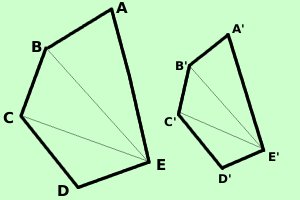 sono simili allora posso scrivere anche Perimetro (ABCDE) : Perimetro(A'B'C'D'E') = AB : A'B' Dimostrazione Essendo i poligoni simili posso scrivere AB : A'B' = BC : B'C' = CD : C'D' = DE : D'E' = EA : E'A' (sono proporzioni valide considerando i rapporti due a due) Posso applicare la proprieta' del comporre posso farlo con una proporzione per volta oppure, per far prima, con tutte le proporzioni insieme (AB+BC+CD+DE+EA) : AB =(A'B'+B'C'+C'D'+D'E'+E'A') : A'B' applico la proprieta' del permutare: scambiando fra loro i medi la proporzione resta valida (AB+BC+CD+DE+EA) : (A'B'+B'C'+C'D'+D'E'+E'A') = AB : A'B' e quindi Perimetro (ABCDE) : Perimetro(A'B'C'D'E') = AB : A'B' come volevamo |

|

|

|

|