|
Problema Il triangolo isoscele ABC ha il perimetro che misura 32 cm, Sapendo che l'altezza relativa al lato obliquo e' 6/5 di quella relativa alla base BC calcolare la misura dell'area del triangolo Per risolvere il problema osserviamo che il punto H e' il punto medio della base e se da esso mando la perpendicolare HN al lato obliquo questa perpendicolare e' la meta' di BK Costruiamo prima di tutto la figura 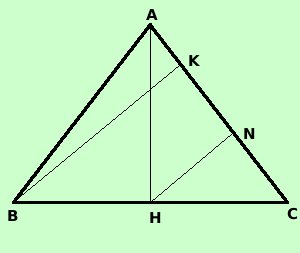
Ponendo AH = x e costruendo HN parallelo a BK ottengo il triangolo HNC simile a BKC e questo mi permettera' di trovare tutti i lati in funzione di AH Pongo AH = x __ BK = 6/5 x__ Dal puno H traccio la parallela HN alla perpendicolare BK ed ottengo il triangolo HNB che e' simile al triangolo BKC, inoltre essendo H il punto medio di AB ne segue che, per il corollario al teorema di Talete, il segmento HN e' la meta' del segmento BK HN = BK/2 = 3/5 x__ __ Considero il triangolo AHN: esso e' rettangolo e posso applicare il teorema di Pitagora per trovare (con la x) il lato AN Nota AH2 = AN2 + NH2 __ __ __
Considero ora il triangolo rettangolo AHC; conosco le misure AN = 4/5 x__ e HN = 3/5 x__ Posso applicare il secondo teorema di Euclide per trovare il valore di NC HN2 = AN · NC __ __ __
questo mi permette di trovare la misura di AC AC = AN + NC = __ __ __ =4/5 x + 9/20 x = 16/20 x + 9/20 x = 25/20 x = 5/4 x Adesso, applicando il primo teorema di Euclide al triangolo AHC, posso trovare il valore di HC HC2 = AC · NC __ __ __
Ottengo quindi BC = 2HC = 6/4x = 3/2 x__ __ Ed essendo AB = AC = 5/4 x __ __ Finalmente posso utilizzare la relazione di partenza AB + BC + AC = 30 cm __ __ __ 5/4 x + 5/4 x + 3/2 x = 30 m.c.m = 4
x = 120 /16 = 15/2 cm = 7,5 cm Abbiamo quindi AH = x __ = 7,5 cm BC = 3/2 x__ = 3/2 · 15/2 cm = 45/4 cm = 11,25 cm E possiamo calcolare l'area
|
||||||||||||||||||||||||||||||||||||||||||