|
Considerato il triangolo rettangolo ABC retto in A, e, dal punto A tracciata la perpendicolare al lato BC sino ad incontrarlo nel punto H, mostrare che i triangoli ABC ed ACH sono simili e scrivere le proporzioni fra i lati corrispondenti Intanto disegniamo la figura: 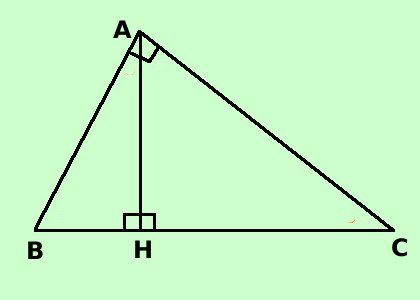 
Mostriamo che sono triangoli simili, utilizzando il primo criterio di similitudine, poi scriviamo la proporzione: Considero i triangoli AHC ed ABC: essi hanno ACH = ACB^ ^perche' angoli coincidenti AHC = BAC^ ^perche' retti per ipotesi Quindi i due triangoli, avendo due angoli congruenti sono simili per il primo criterio di similitudine Metto gli angoli uguali corrispondenti in verticale
ora per scrivere la proporzione prendo due lettere sopra ed in corrispondenza le due lettere sotto: AH : BA = HC : AC = AC : BC o meglio AH :AB = CH : AC = AC : BC |