|
Considerato il triangolo rettangolo ABC retto in A, e, dal punto A tracciata la perpendicolare al lato BC sino ad incontrarlo nel punto H, mostrare che i triangoli ACH ed ABH sono simili e scrivere le proporzioni fra i lati corrispondenti Intanto disegniamo la figura: 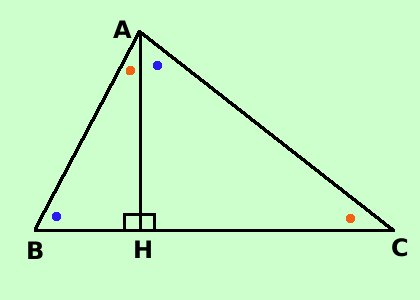
Mostriamo che sono triangoli simili, utilizzando il primo criterio di similitudine, poi scriviamo la proporzione: Considero i triangoli ABH ed AHC: essi hanno BHA = AHC^ ^perche' angoli retti (per ipotesi) Se sommo l'angolo ABH^ con l'angolo BAH^ ottengo un angolo retto Se sommo l'angolo CAH^ con l'angolo BAH^ ottengo ancora un angolo retto Quindi ABH = CAH^ ^perche' complementari dello stesso angolo (cioe' con lo stesso angolo BAH^formano un angolo retto) Quindi i due triangoli, avendo due angoli congruenti sono simili per il primo criterio di similitudine Metto gli angoli uguali corrispondenti in verticale
ora per scrivere la proporzione prendo due lettere sopra ed in corrispondenza le due lettere sotto: AB : CA = BH : AH = AH : CH Da notare che il prendere due lettere sopra e le lettere corrispondenti sotto equivale a prendere segmenti opposti ad angoli uguali: infatti se, ad esempio sono uguali gli angoli H allora nel primo triangolo togliendo H avremo AB e nel secondo togliendo H avremo CA e noi scriviamo AB:CA Togliere H significa prendere il segmento di fronte all'angolo H Se considero A nel primo triangolo ed il suo uguale C nel secondo triangolo allora togliendo A nel primo triangolo ottengo BH e togliendo C nel secondo triangolo ottengo AH quindi scrivo BH:AH In un problema reale prenderemo solo parte della proporzione e precisamente quella parte in cui conosciamo 3 elementi: due elementi del primo triangolo ed uno del secondo (o viceversa) |