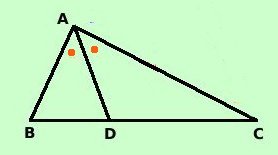
Proprieta' della bisettrice dell'angolo interno di un triangolo Vale il teorema: La bisettrice dell'angolo interno di un triangolo divide il lato opposto in parti proporzionali agli altri due lati So che la retta AD e' la bisettrice dell'angolo BAC; devo dimostrare che vale AB : AC = BD : DC Ipotesi      BAD = DAC^ ^             Tesi AB : AC = BD : DC Dimostrazione: Intuitivamente: dobbiamo far vedere che vale il teorema di Talete, quindi cercheremo, mediante costruzioni, di richiamare la figura del teorema di Talete 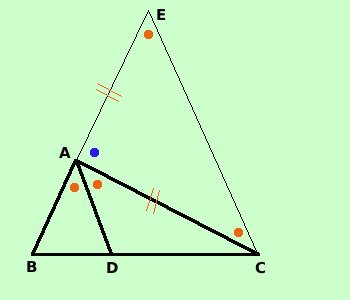Prolungo il segmento BA dalla parte di A di un segmento AE = AC, quindi congiungo E con C. Il triangolo AEC e' isoscele e quindi avremo AEC = ACE ^ ^ Inoltre sappiamo che la somma degli angoli interni di un triangolo vale un angolo piatto cioe' la somma AEC + ACE + CAE^ ^ ^ e' uguale ad un angolo piatto Ma anche l'angolo BAE^=  BAD + DAC + CAE ^ ^ ^ e' uguale ad un angolo piatto ed essendo tutti gli angoli piatti congruenti avremo AEC + ACE + CAE^^^=     BAD + DAC + CAE ^ ^ ^ Possiamo eliminare l'angolo CAE^ da entrembe le parti AEC + ACE^^ =     BAD + DAC^ ^ Ma noi sappiamo che gli angoli AEC^ e ACE^ sono congruenti per costruzione e gli angoli BAD^ e DAC^ sono congruenti per ipotesi Ne deriva che DAC = ACE^^ Essendo gli angoli congruenti DAC^ ed ACE^ angoli alterni interni rispetto alle rette AD e CE ne segue che le rette sono parallele e quindi siamo nelle condizioni del teorema di Talete, pertanto vale: BA : AE = BD : DC Essendo AE = AC posso scrivere AB : AC = BD : DC come volevamo